(Go back to two-way compensation, or back to the introduction)

Let's consider an experiment where we stain human peripheral blood lymphocytes with FITC CD3 (which will stain CD4 and CD8 T cells), and PE CD8 (which will stain CD8 T cells and, less brightly, NK cells). We should have four major populations of cells: (i) B cells, which will be unstained; (ii) CD4 T cells, which will have only fluorescein (CD3) fluorescence; (iii) CD8 T cells, which will have both fluorescein and PE fluorescence; and (iv) NK cells, which will only have PE fluorescence (they do not express CD3). Finally, for the sake of this example, let's pretend that the CD3 fluorescence (FITC) on T cells gives 100 units of true fluorescence (i.e., the amount of fluorescence in FL1 when no compensation is set and no PE had been included in the stain); CD8 fluorescence on CD8 T cells is 400 units, and CD8 on NK is 50 units.

What is the measured fluorescence for each cell, assuming the spillover constants have been measured at 15% and 1% (from the compensation samples)?

For B cells, it will be zero in both FL1 and FL2 (remember, we are ignoring autofluorescence for the time being).

CD4 T cells will have 100 in FL1, and 15 in FL2 (i.e., 15% of the 100 units of fluorescein signal will appear in FL2).

NK cells will have 50 units in FL2, and 0.5 units in FL1 (i.e., 1% of the 10 units of PE signal).

CD8 T cells will have 104 units in FL1 (100 units of fluorescein CD3 signal plus 1% of the 400 units of PE CD8 signal), and 415 units FL2 (400 units of PE signal plus 15% of the 100 units of fluorescein signal).

Let's write this algebraically:

FLx(measured) is the signal actually measured on the cytometer, which is profoundly uninteresting to the biologist; X(true) is the true signal contributed by the fluor--the real value of interest.

These two equations have two unknowns (the true signals), therefore they can be solved exactly. Solving the first equation for FITC(true) gives:

Substitute this into the second equation, and solve for PE(true). We now have:

This gives us the true PE fluorescence from only the measured fluorescences. Once we know this value, we can compute the true FITC fluorescence from the previous equation.

Let's apply these equations to our measured values for CD8 T cells (FL1 = 104, FL2 = 415).

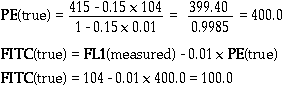
And this is exactly what the CD8 T cells started with! As an exercise, you can work through the remaining cell types to prove to yourself that the math makes it work.

An additional useful exercise would be to run through these calculations, using twice as much FITC signal (but the same PE signal), or half as much; or, to change the compensation values from 15% to, for instance, 50%... get a feel for how the measured values respond to changes in these values.

Afterwards, go on to the three-color section.